Нестационарная задача Навье-Стокса для жидкости с вязкостью

Шестая проблема тысячелетия

Доказательство существования и гладкости решений уравнений Навье-Стокса является шестой задачей тысячелетия. Задача сформулирована Математическим институтом Клэя в 2000 году и описывает движение вязкой ньютоновской жидкости, которая является основой гидродинамики. В работе дано доказательство существования и гладкости решений нестационарной задачи Навье-Стокса с вязкостью. Библиогр. 11 назв.

Публикуется по книге: Омуров Т.Д. Нестационарная задача Навье-Стокса для жидкости с вязкостью/ КНУ им. Ж. Баласагына. – Б.: 2011. – 116 с. Тираж 300 экз.

УДК 532.5.516(04);[517.9]
    ББК 22.253  
    О–57
    ISBN 978–9967–02–759–6
    О 1603040000–11

Основное содержание работы зарегистрировано в Кыргызпатенте: Сектор объектов авторского права, авторское свидетельство №1543 от 30.07.2010 года.

Ответственный редактор: д-р. физ.-мат. наук Каракеев Т.Т.
    Рецензенты: 
    д-р. техн. наук, академик НАН КР Шаршеналиев Ж.Ш.
    д-р. физ.-мат. наук, проф. Саадабаев А.С.
    д-р. физ.-мат. наук, проф. Туганбаев У.М.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ КЫРГЫЗСКОЙ РЕСПУБЛИКИ
    КЫРГЫЗСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ ИМ. Ж. БАЛАСАГЫНА
    Научно-исследовательский центр Навье-Стокса

ОГЛАВЛЕНИЕ

Перечень условных обозначений
    Предисловие 
    Введение

Глава 1. Краткий обзор по исследуемым задачам и математическим понятиям, применяемым в работе

§1.1. Обзор по уравнениям теплопроводности и Пуассона в неограниченной области. Преобразование Фурье
    §1.2. Основные пространства, применяемые в работе для исследования нестационарных задач Навье-Стокса

Глава 2. Нестационарная задача Навье-Стокса для несжимаемой  жидкости

§ 2.1. Задача Навье-Стокса с конвективными членами с условием (а₁)
    §2.2. Предельный случай очень малой вязкости
    §2.3. Решение задачи Навье-Стокса с условием (а₂)
    §2.4. Задача Навье-Стокса с произвольными конвективными членами

Глава 3. Асимптотическое разложение решения уравнения Навье-Стокса с вязкостью

§3.1. Асимптотическое разложение решения течения с трением
    §3.2. Поведение решения системы Навье-Стокса в  при асимптотическом разложении, когда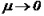 
    §3.3. Интегро-дифференциальные уравнения Навье-Стокса с вязкостью

Глава 4. Нестационарная задача Навье-Стокса для сжимаемого течения изотермического изменения состояния

§4.1. Задача Навье-Стокса для вязкого течения изотермического изменения состояния
    §4.2. Ограниченность решения задачи Навье-Стокса для изотермического изменения состояния в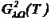 

Заключение
    Задачи для дальнейшего развития изложенной теории
    Аннотация
    Литература
    Дополнительная литература

ПРЕДИСЛОВИЕ

В данной работе исследуется нестационарная задача Навье-Стокса для несжимаемой и сжимаемой жидкости с вязкостью.

Основной целью работы, является доказательство существования, единственности и условной гладкости решения задачи Навье-Стокса для несжимаемой жидкости в ,  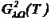или  [или гладкости в ].

Более точно проведены обоснования метода эквивалентного раздробления системы и развита теория о принадлежности решений к конкретным пространствам с весовыми функциями. Рассматривается предельный случай очень малой вязкости в .

Далее, обосновывается справедливость асимптотического разложения, которое позволяет построение решений 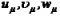 в . При этом изучены особенности решений исследуемых уравнений и методы их построения, и ограниченности в весовых пространствах . В условиях асимптотического разложения при обращении параметра 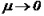 доказывается, что решение системы Навье-Стокса с вязкостью сходится к решению вырожденной системы в смысле  .

Полученные результаты обобщены к интегро-дифференциальным уравнениям Навье-Стокса для несжимаемой жидкости с вязкостью в .

В главе 4 изучена нестационарная задача Навье-Стокса для сжимаемого вязкого течения изотермического изменения состояния в 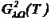, где определяются неизвестные величины: скорость , Р – давление, ρ – плотность.

СКАЧАТЬ полный текст монографии в формате MS Word

Omurov Taalaibek Dardayilovich

Nonstationary Navier-Stokes problem for fluid with viscosity
     Zh.Balasagyn KNU – Bishkek, 2011. – 116p.

Existence and smooth solution of the Navier-Stokes equation is one of the most important problems in mathematics of the century stated by Clay Mathematics Institute in 2000, which describes the motion of viscous Newtonian fluid and which is a basic of hydrodynamic. The chief object of this work is to prove existence and smooth solution of nonstationary problem Navier-Stokes for fluid with viscosity.

Bibliography 11 names

The main content of the work is registered in Kyrgyzpatent: Sector of copyright objects, author’s certificate No. 1543 of 2010/07/30.